دورات الحد. حلقة الحد من الضوضاء التقريبية في الهياكل العودية

عند تحليل الضوضاء الدائرية في المرشحات الرقمية، كان من المفترض أن يكون الفرق بين العينات المتجاورة لإشارة الدخل كبيرًا مقارنة بخطوة التكميم. سمح لنا هذا بافتراض أن عينات الضوضاء التقريبية كانت غير مرتبطة ببعضها البعض ومع عينات تسلسل الإدخال. ومن الواضح أنه في كثير من الحالات (على سبيل المثال، إذا كانت إشارة الدخل ثابتة أو صفر) فإن هذا الافتراض غير صحيح.

دعونا ننظر كمثال على معادلة الفرق

ونفترض أن تسلسل الإدخال (أي تم تعطيل إدخال المرشح) والشرط الأولي هو (يتم التعبير عن قيم المتغير y بوحدات خطوة التكميم Q وبالتالي لا يمكن أن تكون كسرية.) يقارن الجدول أدناه القيم الدقيقة المحسوبة وفق المعادلة (5.122)، دون استخدام التقريب، وكذلك القيم المتحصل عليها من الحسابات مع التقريب.

على الرغم من أن القيم الدقيقة تميل بشكل كبير إلى الصفر، إلا أنه عند استخدام التقريب، يتم "تشديد" القيم إلى مستوى 10 ولا يمكن تغييرها أكثر. يوضح المثال المدروس حدوث تأثير دورة الحد في مرشح رقمي متكرر بإشارة دخل صفر. أطلق بلاكمان على فترات الاتساع التي تحدث فيها تأثيرات الدورة الحدية مناطق ميتة. في المثال الذي تم النظر فيه، لأي شيء سوف يتبين أنه إذا . وبالتالي، فإن الفاصل الزمني هو منطقة ميتة.

درس جاكسون الدورات الحدية في أنظمة الدرجة الأولى والثانية باستخدام مفهوم "القيم الفعالة" لمعاملات المرشح، أي مع الأخذ في الاعتبار أن الدورات الحدية تحدث فقط عندما يؤدي التقريب فعليًا إلى ظهور أقطاب على دائرة الوحدة. وبالتالي، بالنسبة للنظام الموصوف بمعادلة فرق من الدرجة الأولى

حيث يشير الرمز إلى عملية التقريب إلى أقرب عدد صحيح، وبالنسبة للمنطقة الميتة التي يمكن أن توجد فيها الدورات الحدية هي الفاصل الزمني، وk يساوي أكبر عدد صحيح يحقق المتراجحة

(5.124)

ويترتب على المثال أعلاه أنه بالنسبة للعينات السالبة عند مخرج المرشح في وضع الدورة الحدية، يكون لها سعة وإشارة ثابتة. إذا، فإن قراءات الخرج في وضع دورة الحد سيكون لها سعة ثابتة، ولكن بإشارة متناوبة. بالنسبة لجميع القيم داخل المنطقة الميتة، فإن القيمة الفعالة للعامل a تساوي ±1، أي. وبالتالي فإن معادلة الفرق (5.123) تقابل قطبًا فعالًا عند النقطة .

لنظام من الدرجة الثانية موصوف بمعادلة الفرق

المنطقة الميتة التي يمكن أن تحدث فيها تأثيرات الدورة الحدية هي الفاصل الزمني، حيث k هو أكبر عدد صحيح يحقق المتراجحة

(5.126)

الصيغة (5.126) تشبه الصيغة (5.124)، ولكن يتم استبدالها بـ . عند استيفاء العلاقة (5.126)، فإن أقطاب المرشح تقع بالتأكيد على دائرة الوحدة، أي أن القيمة الفعالة هي 1.0. (لاحظ أنه عند ، ستكون الأقطاب مترافقة بشكل معقد وسيكون المرشح مستقرًا.) يتم تحديد تردد التذبذب في وضع الدورة المحدودة بشكل أساسي من خلال القيمة ولكنه يعتمد أيضًا على كيفية تأثير التقريب على قيمة المنتج في الصيغة (5.125) .

ويترتب على الصيغة (5.126) أن أصغر قيمة يتشكل عندها زوج من الأقطاب المترافقة المعقدة الفعالة هي 0.5. في هذه الحالة، القيمة التالية التي تحدث لها تأثيرات دورة الحد عند قيمة أكبر هي 0.75. في هذه الحالة، أو 2. بالنسبة لأي قيمة، لا يوجد سوى عدد محدود من فترات القيم التي يمكن أن تحدث لها تأثيرات دورة حدية مختلفة. المناطق المقابلة في المستوى لكتلة الرتبة الثانية الموصوفة بالمعادلة (5.125) موضحة في الشكل. 5.42. يتم تمييز المنطقة التي لا تحدث فيها الدورات الحدية بالتظليل. تتوافق الخطوط الأفقية مع الحد الأدنى من القيم التي يتغير عندها الوضع في المنطقة الميتة. تشير الأرقام الموجودة داخل كل منطقة إلى القيمة القصوى لسعة التذبذبات في وضع الدورة الحدية الممكنة في هذه المنطقة من المستوى.

تين. 5.42. اعتماد سعة تذبذب الدورة الحدية على معاملات المرشح (حسب جاكسون).

سيتم مناقشة الدورات الحدية الناشئة أدناه.

أعلاه، قمنا بتحليل تأثيرات الدورة الحدية في كتل الدرجة الثانية، المقابلة لظهور زوج من الأقطاب المترافقة المعقدة الفعالة. يمكن أن توجد دورات الحد في مثل هذه الكتل أيضًا عندما يظهر قطب فعال حقيقي عند النقطة z = ±1. في هذه الحالة، شرط حدوث وضع دورة الحد مع سعة الإخراج يساوي k هو المساواة التالية:

بالنسبة لقيم مختلفة لـ k، ليس من الصعب تحديد موضع المناطق في المستوى الذي يتم استيفاء الشرط (5.127) فيه. وتظهر هذه المناطق في الشكل. 5.42.

دراسة الدورات الحدية مهمة لسببين. في أنظمة الاتصالات، يمكن أن يؤدي فقدان الإشارة إلى تأثيرات حلقة الحد. وهذا أمر غير مرغوب فيه إلى حد كبير، لأنك ترغب في التأكد من أنه في حالة عدم وجود إشارة دخل، فلن يتم سماع أي شيء عند إخراج القناة. لذلك، عند استخدام المرشحات الرقمية في أنظمة الهاتف، يجب إيلاء هذه المشكلة اهتماما خطيرا للغاية. السبب الثاني هو أنه يمكن استخدام الدورات الحدية لإنشاء تسلسلات دورية. يمكن استخدام تذبذبات الدورة المحدودة بالخصائص المطلوبة في المعالجة الرقمية كمصدر للإشارة.

بعد نشر أعمال جاكسون حول الدورات الحدية، تم إيلاء الكثير من الاهتمام لتوضيح حدود اتساع وترددات تذبذبات الدورة الحدية. يمكن العثور على التفاصيل في المنشورات ذات الصلة.

الأدب

الأدب العام

1. أوبنهايم إيه في، وينشتاين إس دبليو، تأثيرات طول السجل المحدود في المرشحات الرقمية وتحويل فورييه السريع، بروك. معهد مهندسي الكهرباء والإلكترونيات، 60، لا. 8، 957-976 (أغسطس 1972)؛ هناك ترجمة روسية: أوبنهايم، وينشتاين، تأثير طول السجل المحدود في الترشيح الرقمي وتحويل فورييه السريع، TIIER، المجلد 60، رقم 8، الصفحات من 41 إلى 65 (1972).

2. Gold V., Rader S. M.، المعالجة الرقمية للإشارات، الفصل. 4، ماكجرو هيل، 1969؛ هناك ترجمة روسية: Gold B., Rader Ch., معالجة الإشارات الرقمية، دار النشر الإذاعية السوفيتية، 1973.

3. ليو دبليو، تأثير طول الكلمة المحدود على دقة المرشحات الرقمية - مراجعة، IEEE Trans. نظرية الدائرة، CT-18، 670-677 (نوفمبر 1971).

4. بينيت دبليو آر، أطياف الإشارات الكمية، نظام بيل. تقنية. ج.، 27، 446-472 (يوليو 1948).

5. Rader S. M., Gold V., تأثيرات تكميم المعلمات على أقطاب المرشح الرقمي، Proc. معهد مهندسي الكهرباء والإلكترونيات، 55، لا. 5، 688-689 (مايو 1967)؛ هناك ترجمة روسية: رايدر، جولد، تأثير تكميم المعلمات على أقطاب المرشح الرقمي، TIIER، 55، رقم 55، ص 98-100 (1967).

تقريب الضوضاء في الهياكل العودية. حالة النقطة الثابتة

1. نولز جيه دبليو، إدواردز ر.، تأثيرات حاسوب محدد طول الكلمات في نظام التغذية المرتدة للبيانات Sainpled، بروك. انست. كهربائي. المهندس، 112، 1197-1207 (يونيو 1965).

2. Gold V., Rader S. M.، تأثيرات ضوضاء التكميم في المرشحات الرقمية، بروك. AFIPS 1966 مؤتمر الربيع المشترك للكمبيوتر، 28، 213-219 (1966).

3. جاكسون إل في، حول تفاعل الضوضاء الدائرية والمدى الديناميكي في المرشحات الرقمية، نظام بيل. تقنية. ج.، 49، 159-184 (فبراير 1970).

4. جاكسون إل دبليو، تحليل الضوضاء الدائرية للمرشحات الرقمية ذات النقاط الثابتة التي يتم تحقيقها في شكل متتالي أو متوازي، IEEE Trans، حول الصوت والصوتيات الكهربائية، AU-18، 107-122 (يونيو 1970).

يتم تقريب الضوضاء في الهياكل غير العودية. حالة النقطة الثابتة

1. تشان دي إس كيه، رابينر إل آر، نظرية الضوضاء المستديرة في الإنجازات المتتالية للمرشحات الرقمية للاستجابة النبضية المحدودة، نظام بيل. تقنية. ج.، 52، رقم. 3، 329-345 (مارس 1973).

2. تشان دي إس كيه، رابينر إل آر، خوارزمية لتقليل ضوضاء التقريب في الإنجازات المتتالية للمرشحات الرقمية ذات الاستجابة النبضية المحدودة، نظام بيل. تقنية. ج.، 52، رقم. 3، 347-385 (مارس 1973).

3. تشان د.س.ك.، رابينر إل.ر.، تحليل أخطاء القياس الكمي في النموذج المباشر للمرشحات الرقمية للاستجابة النبضية المحدودة، IEEE Trans، في الصوت والصوتيات الكهربائية، AU-21، رقم. 4، 354-366 (أغسطس 1973).

تقريب الضوضاء في الهياكل العودية. حالة النقطة العائمة

1. ساندبرج آي دبليو، تراكم تقريب النقطة العائمة في تحقيق المرشح الرقمي، نظام بيل. تقنية. ج.، 46، 1775-1791 (أكتوبر 1967).

2. Kapeko T., Liu V.، خطأ التقريب للمرشحات الرقمية ذات النقطة العائمة، Proc. Ш مؤتمر أليرتون السنوي. في نظرية الدائرة والنظام، 219-227 (أكتوبر 1968).

3. وينشتاين سي.، أوبنهايم إيه في، مقارنة بين ضوضاء التقريب في النقطة العائمة وتحقيقات المرشح الرقمي للنقطة الثابتة، بروك. IEEE (Corrsp.)، 57، 1181-1183 (يونيو 1969)؛ هناك ترجمة روسية: Weinshtepn، Oppenheim، مقارنة تقريب الضوضاء للمرشحات الرقمية مع تنفيذ PH باستخدام طريقة النقطة العائمة وطريقة النقطة الثابتة، TIIER، المجلد 57، رقم 7. الصفحات 72-74 (1969).

4. ليو في، كابيكو تي، تحليل الأخطاء في المرشحات الرقمية باستخدام حساب النقطة العائمة، بروك. IEEE، 57، 1735-1747 (أكتوبر 1969)؛ هناك ترجمة روسية: ليو، كانيكو، تحليل الأخطاء للمرشحات الرقمية التي يتم تنفيذها من خلال العمليات الحسابية للفاصلة العائمة، TIIER، المجلد 57، رقم 10، الصفحات من 49 إلى 63 (1969).

5. أوبنهايم إيه في، تحقيق المرشحات الرقمية باستخدام حساب النقاط العائمة، IEEE Trans، في الصوت والصوتيات الكهربائية، AU-18، 130-136 (يونيو 1970).

تقلبات الفائض

1. إيبرت بي إم، مازو جي إي، تايلور إم جي، التذبذبات الفائضة في المرشحات الرقمية، نظام بيل. تقنية. ج.، 48، 3021-3030 (نوفمبر 1968).

تكميم المعاملات في الهياكل العودية

2. كايزر جي إف، بعض الاعتبارات العملية في تحقيق المرشحات الرقمية الخطية، بروك. مؤتمر أليرتون السنوي الثالث. في نظرية الدوائر والأنظمة، 621 - 633 (1965).

3. Rader S. M., Gold V., تأثيرات تكميم المعلمات على أقطاب المرشح الرقمي، Proc. IEEE (كورسب.)، 55، 688-689 (مايو 1967).

4. نولز جي في، أولكايتو إي إم، دقة المعامل واستجابة المرشح الرقمي، IEEE Trans. نظرية الدائرة، 15، لا. 1، 31-41 (مارس 1968).

5. Avenhaus E., Schuessler H. W.، حول مشكلة التقريب في تصميم المرشحات الرقمية ذات طول الكلمات المحدود، Arch. إليك. أوبرتراجونج، 24، 571-572 (1970).

تكميم المعاملات في الهياكل غير العودية

1. هيرمان أو.، شوسلر إن دبليو، حول مشكلة الدقة في تصميم المرشحات الرقمية غير العودية، القوس. إليك. أوبرتراجونج، 24، 525-526 (1970).

2. تشان د.س.ك.، رابينر إل.ر.، تحليل أخطاء القياس الكمي في النموذج المباشر للمرشحات الرقمية للاستجابة النبضية المحدودة، IEEE Trans، في الصوت والصوتيات الكهربائية، AU-21، رقم. 4، 354-366 (أغسطس 1973).

3. سي دبليو وينشتاين، تأثيرات القياس الكمي في مرشحات أخذ عينات التردد، سجل NEREM، 22 (1968).

دورات الحد في الهياكل العودية

1. بلاكمان آر دبليو، تجانس البيانات الخطية والتنبؤ في النظرية والتطبيق، أديسون ويسلي بوهل. شركة، ريدينغ، ماساشوستس، ص. 75-79 (1965).

2. جاكسون إل في، تحليل دورات الحد بسبب تقريب الضرب في المرشحات الرقمية العودية (الفرعية)، بروك. مؤتمر أليرتون السنوي الأول. حول نظرية الدائرة والنظام، 69-78 (1969).

3. باركر إس آر، هيس إس إف، تذبذبات الدورة المحدودة في المرشحات الرقمية، IEEE Trans. نظرية الدائرة، CT-18، 687-696 (نوفمبر 1971).

4. ساندبرج آي دبليو، نظرية تتعلق بالدورات الحدية في المرشحات الرقمية، بروك. مؤتمر أليرتون السابع. حول نظرية الدائرة والنظام، 63-67 (1969).

5. بروبكر تي إيه، جودي جي إن، الحد من الدورات في المرشحات الرقمية، IEEE Trans. التحكم الآلي، 17، رقم. 5، 675-677 (أكتوبر 1972).

6. ساندبرج 1. دبليو، كايزر جي إف، ربط الدورات المحدودة في تطبيقات النقاط الثابتة للمرشحات الرقمية، IEEE Trans، في الصوت والصوتيات الكهربائية، AU-20، رقم. 2، 110-112 (يونيو 1972).

متحرك أنظمة تصور الدورية حركة. على مقربة من P. ج. إما الابتعاد عنه (P. ts. غير المستقر) ، أو الاقتراب منه إلى أجل غير مسمى - "ينتهي" عليه (P. ts المستقر). سلوك المسارات في محيط P. c. يرتبط بقيم مضاعفاته (انظر. التشعب).إذا القيمة المطلقة. تكون قيم جميع المضاعفات أقل من 1، فتقترب منه جميع المسارات بلا حدود وهو مستقر. مقاومة P. ج. هي الرياضيات. بشكل دوري. التذبذبات الذاتية. على سبيل المثال، تحتوي معادلة فان دير بول (التي تصف، على وجه الخصوص، ديناميكيات مذبذب الأنبوب) على PC واحد ثابت لقيم المعلمات > 0. (رسم بياني 1).

أرز. 1. صور الطور لمولد فان دير بول بقيم غير خطية مختلفة: أ- شبه متناغم. 6 - بقوة غير جيبية. الخامس- استرخاء.

بالنسبة للأنظمة ذات درجة واحدة من الحرية (مساحة الطور الخاصة بها عبارة عن مستوى) P. c. وتستنفد حالات التوازن المستقرة جميع الأجسام المحتملة التي تجذب المسارات المجاورة على مستوى الطور. في ديناميكية متعددة الأبعاد الأنظمة ذات البعد الفضائي الطوري ن 3، من الممكن جذب أشياء أكثر تعقيدًا - عوامل جذب.

أرز. 2. دورة حد السرج: - مشعب فصل مستقر. - مشعب فصل غير مستقر.

إذا كانت بعض المضاعفات (وليس كلها) أكبر من 1 في القيمة المطلقة، فإن P. c. سرج (الشكل 2) ويقع عند تقاطع مشعبتين منفصلتين: واحدة مستقرة، تقترب من خلالها المسارات من P. c.، وواحدة غير مستقرة، تتكون من مسارات تتحرك بعيدًا عن P. c. مسارات. أصناف مستقرة من P. ج. يمكن أن ينفصل في مرحلة الفضاء مناطق الجذب المختلفة. عوامل الجذب - بسيطة (حالة التوازن، PC مستقرة) وغريبة. المتشعبات غير المستقرة للسرج P. ج. قد يتم تضمينها في عوامل جذب غريبةوالعشوائية. مجموعات الأنظمة الهاملتونيةوتحديد بنيتها. إذا كانت جميع المضاعفات أكبر من 1 في القيمة المطلقة، فإن P. c. غير مستقر (مستقر عند عكس اتجاه الحركة على طول المسار، أي متى).

دورة الحد هي منحنى مغلق معزول على مستوى الطور والذي في الحد حيث t ® ¥ تميل جميع المنحنيات المتكاملة . تمثل الدورة الحدية نظامًا ثابتًا بسعة معينة، مستقلة عن الظروف الأولية، ولكن يتم تحديدها فقط من خلال تنظيم النظام. إن وجود دورة حدية على مستوى الطور هو السمة الرئيسية لنظام التأرجح الذاتي. من الواضح أنه في عملية التذبذب الذاتي، يمكن أن تكون مرحلة التذبذب موجودة.

دعونا نتناول الخصائص العامة للأنظمة ذاتية التأرجح. لنفكر في نظام المعادلات العامة:

إذا كان T (T > 0) هو أصغر رقم لأي t

فإن التغير في المتغيرات x = x(t), y = y(t) يسمى تغيرًا دوريًا مع الفترة T .

يتوافق التغيير الدوري مع مسار مغلق على مستوى الطور، والعكس صحيح: لأي مسار مغلق هناك مجموعة لا حصر لها من التغييرات الدورية، تختلف عن بعضها البعض في اختيار النقطة المرجعية الزمنية.

إذا كان التغيير الدوري على مستوى الطور يتوافق مع منحنى مغلق معزول، يتم الاقتراب منه من الخارج والداخل (مع زيادة ر) المسارات المجاورة على طول اللوالب، هذا المسار المغلق المعزول هو دورة محدودة.

تتيح الأمثلة البسيطة التحقق من أن النظام العام (8.1) يقبل الدورات المحدودة كمسارات.

على سبيل المثال، للنظام

(8.2)

المسار هو دورة الحد. معادلاتها البارامترية ستكون:

وسيتم كتابة معادلات جميع مسارات الطور الأخرى بالصيغة:

التكامل القيم الثابتة مع> 0 تتوافق مع مسارات الطور التي تلتف حول دورة الحد من الداخل (عند ر®¥)، والقيم –1<ج<0 траектории, накручивающиеся снаружи.

يقال إن الدورة الحدية مستقرة إذا كانت هناك منطقة على مستوى الطور تحتوي على دورة الحد هذه، وهي منطقة e، بحيث تقترب جميع مسارات الطور التي تبدأ في جوار e بشكل مقارب من دورة الحد مثل t ® ¥.

على العكس من ذلك، إذا كان هناك في أي حي صغير بشكل تعسفي e من الدورة الحدية مسار طور واحد على الأقل لا يقترب من الدورة الحدية عند t ® ¥، فإن دورة الحد هذه تسمى غير مستقرة . تفصل مثل هذه الدورات مناطق التأثير (المجموعات) لمجموعات الجذب المختلفة.

في التين. 8.2 يظهر دورة حدية مستقرة ( أ) وغير مستقر ( ب) و ( الخامس).

دورات الحد غير المستقرة مثل تلك الموضحة في الشكل. 8.2 ببحيث تقترب منها جميع المسارات من جهة (من الداخل مثلاً) وتبتعد عنها من الجهة الأخرى (من الخارج مثلاً) عندما ر® ¥ تسمى "شبه مستقرة" أو مزدوجة. يرجع الاسم الأخير إلى حقيقة أن هذه الدورات عادةً، مع تغيير مناسب في معلمة النظام، يتم تقسيمها إلى قسمين، أحدهما مستقر والآخر غير مستقر.

أكون. أظهر ليابونوف ذلك لدراسة استقرار الحركة الدورية س =ي( ر), ص=ذ( ر) يمكنك اتباع مسار خطية المعادلات، تمامًا كما فعلنا عند دراسة استقرار حالات التوازن. إذا وضعت

استبدل هذه التعبيرات في معادلات (8.1)، وقم بتوسيع الأطراف اليمنى لهذه المعادلات - الدوال

في سلسلة بقدرات x و h وتجاهل المصطلحات غير الخطية، ثم نحصل على معادلات خطية (معادلات التقريب الأول) لإحداثيات الاضطراب x و h:

المعاملات على الجانب الأيمن:

هذا نظام من المعادلات التفاضلية الخطية ذات معاملات الدورة الدورية ت، بسبب ال أ, ب, ج, دجوهر وظائف j، y - الوظائف الدورية للوقت مع فترة ت. نظرة عامة على حلها

فيما يلي بعض الوظائف الدورية مع الفترة ت. تعتمد خصائص حلول الانحرافات عن الحل الدوري الثابت x و h على المؤشرات والتي تسمى "المؤشرات المميزة". أي أن علامات أجزائها الحقيقية تحدد ما إذا كانت هذه الحلول تتزايد أم تتناقص. يمكن إثبات أنه بسبب استقلالية النظام الأصلي (8.1)، فإن أحد المؤشرات المميزة يساوي الصفر، والآخر يساوي ح.

أين س= ي( ر), ذ= ص( ر) - أي حل دوري يتوافق مع الدورة الحدية قيد النظر، ت- فترة القرار.

وبالتالي، فإن استقرار دورة الحد (والاستقرار بمعنى ليابونوف للحركات الدورية المقابلة) يتم تحديده من خلال علامة الأس المميزة. دورة الحد مستقرة إذا ح < 0 и неустойчив, если ح> 0. إذا ح= 0، معادلات التقريب الأول لا تحل مسألة استقرار الحركة الدورية.

للعثور على دورات نهاية، لا توجد طرق تحليلية بسيطة مثل العثور على النقاط الثابتة ودراسة استقرارها. ومع ذلك، فإن دراسة مستوى الطور لنظام ما تسمح لنا بالإجابة على سؤال ما إذا كانت هناك دورة حدية في نظام معين أم لا.

دعونا نقوم بصياغة العديد من النظريات التي تحدد وجود دورة حدية بناءً على البنية الطوبولوجية لمستوى الطور. يمكن أن تكون مفيدة في كل من التحليل التحليلي والحاسوبي للنظام.

النظرية 1. يجب أن تكون هناك منطقة على مستوى الطور لا تخرج منها مسارات الطور، ولا توجد فيها مواقع توازن (نقاط فردية). ومن ثم توجد بالضرورة دورة حدودية في هذه المنطقة، وتلتف جميع المسارات الأخرى حولها بالضرورة.

في التين. 8.3. تم تصوير هذه المنطقة ز، والتي لا تخرج منها مسارات الطور. وهذا يعني أن مسارات الطور إما أن تدخل المنطقة عن طريق عبور الحدود، أو أن الحدود نفسها هي مسار. ومن السهل أن نرى أن مثل هذه المنطقة لا يمكن ربطها ببساطة. نظرًا لأن المسار يلتف حول الدورة الحدية من الداخل، فهذا يعني أنه داخل هذه الدورة الحدية على مستوى الطور توجد إما نقطة مفردة غير مستقرة أو دورة حدية غير مستقرة، ومن الواضح أنها لا تنتمي إلى المنطقة قيد النظر ز.

وبالتالي، إذا وجدنا منطقة متصلة بشكل مزدوج على مستوى الطور بحيث تكون اتجاهات مسارات الطور على طول الحد بأكمله موجهة داخل هذه المنطقة، فيمكننا أن ندعي أن هناك دورة نهاية داخل هذه المنطقة.

النظرية 2.إذا كانت هناك منطقة مغلقة على مستوى الطور بحيث تدخل جميع مسارات الطور التي تعبر حدود هذه المنطقة، ويوجد داخل هذه المنطقة نقطة مفردة غير مستقرة، فإن هذه المنطقة بالضرورة لها دورة حدية واحدة على الأقل(الشكل 8.4)

نقدم أيضًا بعض المعايير لغياب مسارات المرحلة المغلقة (بما في ذلك الدورات الحدية).

1. إذا لم تكن هناك نقاط مفردة في النظام، فلا يمكن أن يكون هناك مسارات طور مغلقة فيه.

2. إذا كان هناك نقطة واحدة فقط في النظام، تختلف عن العقدة والتركيز والمركز (على سبيل المثال، السرج)، فإن هذا النظام لا يسمح بمسارات الطور المغلق.

3. إذا كان النظام يحتوي فقط على نقاط مفردة بسيطة، ومن خلال جميع نقاط العقدة ونوع التركيز هناك منحنيات متكاملة تصل إلى ما لا نهاية، فلا توجد مسارات طور مغلقة في مثل هذا النظام.

إذا تم استيفاء المعايير 1-3، يمكننا أن نقول بثقة أنه لا توجد دورات الحد في النظام. ومع ذلك، فإن الفشل في تلبية هذه المعايير لا يسمح لنا بعد باستخلاص استنتاج حول وجود دورات محدودة، وبالتالي التذبذبات الذاتية في النظام.

يمكن أيضًا تضمين دورة حدية غير مستقرة في صورة الطور للأنظمة التقريبية. ومع ذلك، فإن دورة الحد هذه لا تتوافق مع عملية دورية حقيقية؛ فهي تلعب فقط دور "مستجمع المياه"، حيث يكون للمسارات سلوك مختلف على كلا الجانبين. على سبيل المثال، في الشكل. يمثل الشكل 8.5 فاصلًا يفصل منطقة مسارات الجاذبية إلى نقطة مفردة مستقرة من ناحية، وإلى دورة حدية مستقرة من ناحية أخرى.

المحاضرة 8

التذبذبات في النظم البيولوجية

مفهوم التذبذبات الذاتية صورة لنظام التأرجح الذاتي على مستوى الطور. دورات الحد. شروط وجود دورات الحد. ولادة دورة الحد. تشعب أندرونوف-هوبف. الإثارة الناعمة والصعبة للاهتزازات. نموذج بروسيلاتور أمثلة على نماذج التذبذب الذاتي للعمليات في الأنظمة الحية. تقلبات في العمليات المظلمة لعملية التمثيل الضوئي. التذبذبات الذاتية في نموذج تحلل السكر. التقلبات داخل الخلايا في تركيز الكالسيوم. دورات الخلية.

تتميز النظم البيولوجية بالتغيرات الدورية في مختلف الخصائص. قد ترتبط فترة هذه التقلبات بالتغيرات الدورية في الظروف المعيشية على الأرض - تغير الفصول، وتغير النهار والليل. هناك إيقاعات جيوفيزيائية أخرى - شمسية، قمرية، مرتبطة بفترات الظواهر الجوية. تتم مقارنة الإيقاعات الجيوفيزيائية والبيولوجية في الشكل 1. 8.1. لكن العديد من العمليات الدورية لها تكرار للتغيير لا يرتبط بشكل واضح بالدورات الجيوكونية الخارجية. هذه هي ما يسمى بـ "الساعات البيولوجية" ذات الطبيعة المختلفة، بدءًا من اهتزازات الجزيئات الحيوية، والاهتزازات الكيميائية الحيوية، وحتى الموجات السكانية.

تحدد الاهتزازات داخل الخلايا إيقاعات بيولوجية داخلية تتميز بها جميع الأنظمة الحية. وهي تحدد وتيرة انقسام الخلايا وتقيس وقت ولادة وموت الكائنات الحية. تُستخدم نماذج الأنظمة التذبذبية في التحفيز الأنزيمي ونظرية المناعة ونظرية نقل الأيونات عبر الغشاء وعلم الأحياء الدقيقة والتكنولوجيا الحيوية.

لقد سبق أن تناولنا بعض أنواع الحركات الدورية عند النظر في النقاط المفردة مثل المركز والذبذبات المضمحلة أو المتزايدة في حالة البؤرة المستقرة وغير المستقرة. إلا أن "الساعة البيولوجية" لها خاصية تميزها عن أنواع التذبذبات المعنية- الدورة الثابتة والسعة مع مرور الوقتمثل هذه التقلبات، وهذا يعني ثبات واستقرار الوضع التذبذب.

أرز. 8.1.الإيقاعات الكونية والجيوفيزيائية والبيولوجية. على اليمين يوجد مقياس الفترة، وعلى اليسار يوجد مقياس التكرار

في هذه الحالة، تمثل التغيرات الدورية في الكميات أحد أنواع السلوك الثابت للنظام. إذا كانت التذبذبات في النظام لها فترة ثابتة وسعة ثابتة، ويتم إنشاؤها بغض النظر عن الظروف الأولية ويتم الحفاظ عليها بسبب خصائص النظام نفسه، وليس بسبب تأثير القوة الدورية، يسمى النظام تتأرجح ذاتيًا.

تكون التذبذبات غير المخمدة في مثل هذه الأنظمة مستقرة، حيث يتم إخماد الانحرافات عن نظام التذبذب الثابت. تشمل فئة الأنظمة ذاتية التذبذب التقلبات في تحلل السكر والأنظمة الأيضية الأخرى، والعمليات الدورية لعملية التمثيل الضوئي، والتقلبات في تركيز الكالسيوم في الخلية، والتقلبات في عدد الحيوانات في السكان والمجتمعات.

دورة الحد. في فضاء الطور، يتوافق هذا النوع من السلوك مع مجموعة جاذبة (جاذبة)، تسمى دورة الحد.

دورة الحد هي منحنى مغلق معزول على مستوى الطور، والذي يصل إلى الحد عند t ® ¥ تميل جميع المنحنيات المتكاملة إلى . تمثل الدورة الحدية نظامًا ثابتًا بسعة معينة، مستقلة عن الظروف الأولية، ولكن يتم تحديدها فقط من خلال تنظيم النظام. إن وجود دورة حدية على مستوى الطور هو السمة الرئيسية لنظام التأرجح الذاتي. من الواضح أنه في عملية التذبذب الذاتي، يمكن أن تكون مرحلة التذبذب موجودة.

دعونا نتناول الخصائص العامة للأنظمة ذاتية التأرجح. لنفكر في نظام المعادلات العامة:

(8.1)

إذا كان T (T > 0) هو أصغر رقم لأي t

ثم تغيير المتغيرات س= س( ر), ذ= ذ( ر) يسمى التغيير الدوري مع الفترة T .

تتيح الأمثلة البسيطة التحقق من أن النظام العام (8.1) يقبل الدورات المحدودة كمسارات.

على سبيل المثال، للنظام

(8.2)

المسار هو دورة الحد. معادلاتها البارامترية ستكون:

وسيتم كتابة معادلات جميع مسارات الطور الأخرى بالصيغة:

التكامل القيم الثابتة مع > 0 يتوافق مع مسارات الطور التي تتجه نحو دورة الحد من الداخل (عند ر ® ¥ )، والقيم -1 < ج < 0 مسارات الرياح من الخارج.

يقال إن الدورة الحدية مستقرة إذا كانت هناك منطقة على مستوى الطور تحتوي على هذه الدورة الحدية، - حيّه ، أن جميع مسارات المرحلة تبدأ في المنطقة المجاورة ه ، مقارب في ر ® ¥ يقترب من دورة الحد.

إذا، على العكس من ذلك، في أي حي صغير بشكل تعسفي ه دورة الحد يوجد مسار طور واحد على الأقل لا يقترب من دورة الحد عند t ® ¥ ، فإن دورة الحد هذه تسمى غير مستقرة . تفصل مثل هذه الدورات مناطق التأثير (المجموعات) لمجموعات الجذب المختلفة.

في التين. 8.2 يظهر دورة حدية مستقرة ( أ) وغير مستقر ( ب) و ( الخامس).

دورات الحد غير المستقرة مثل تلك الموضحة في الشكل.8.2 ببحيث تقترب منها جميع المسارات من جهة (من الداخل مثلاً) وتبتعد عنها من الجهة الأخرى (من الخارج مثلاً) عندمار® ¥ ، تسمى "شبه مستقرة" أو مزدوجة. يرجع الاسم الأخير إلى حقيقة أن هذه الدورات عادةً، مع تغيير مناسب في معلمة النظام، يتم تقسيمها إلى قسمين، أحدهما مستقر والآخر غير مستقر.

أكون. أظهر ليابونوف ذلك لدراسة استقرار الحركة الدورية س =ي(ر), ص=ذ(ر) يمكنك اتباع مسار خطية المعادلات، تمامًا كما فعلنا عند دراسة استقرار حالات التوازن. إذا وضعت

استبدل هذه التعبيرات في معادلات (8.1)، ثم قم بتوسيع الأطراف اليمنى لهذه المعادلات - المهام

مرتبة حسب الدرجاتسو حونتخلص من الحدود غير الخطية فنحصل على معادلات خطية (معادلات تقريبية أولى) لإحداثيات الاضطرابسو ح:

المعاملات على الجانب الأيمن:

هذا نظام من المعادلات التفاضلية الخطية ذات معاملات الدورة الدورية ت، بسبب ال أ, ب, ج, دجوهر الوظيفة مني, ذ- الوظائف الدورية للوقت مع الفترة ت. نظرة عامة على حلها

هنا - بعض الوظائف الدورية مع الفترة ت. تعتمد خصائص حلول الانحرافات عن الحل الدوري الثابت على المؤشرات التي تسمى "المؤشرات المميزة"سو ح. أي أن علامات أجزائها الحقيقية تحدد ما إذا كانت هذه الحلول تتزايد أم تتناقص. يمكن إثبات أنه بسبب استقلالية النظام الأصلي (8.1)، فإن أحد المؤشرات المميزة يساوي الصفر، والآخر يساوي ح.

أين س= ي(ر), ذ= ذ(ر) - أي حل دوري يتوافق مع الدورة الحدية قيد النظر، ت- فترة القرار.

وبالتالي، فإن استقرار دورة الحد (والاستقرار بمعنى ليابونوف للحركات الدورية المقابلة) يتم تحديده من خلال علامة الأس المميزة. دورة الحد مستقرة إذا ح < 0 وغير مستقر إذا ح > 0. إذا ح = 0، معادلات التقريب الأولى لا تحل مسألة استقرار الحركة الدورية.

نظريةأ 1. يجب أن تكون هناك منطقة على مستوى الطور لا تخرج منها مسارات الطور، ولا توجد فيها مواقع توازن (نقاط فردية). ومن ثم توجد بالضرورة دورة حدودية في هذه المنطقة، وتلتف جميع المسارات الأخرى حولها بالضرورة.

نقدم أيضًا بعض المعايير لغياب مسارات المرحلة المغلقة (بما في ذلك الدورات الحدية).

1. إذا لم تكن هناك نقاط مفردة في النظام، فلا يمكن أن يكون هناك مسارات طور مغلقة فيه.

ولادة دورة الحد. تشعب أندرونوف-هوبف.

إن وجود دورات حدية ممكن فقط في نظام من النوع (8.1)، حيث يتم تمثيل الجوانب اليمنى منه بوظائف غير خطية.

في مخطط التشعب 4.11، رأينا أنه عند عبور المحور السيني، يتغير استقرار التركيز. تتوافق القيم الصفرية للجزء الحقيقي من الأعداد المميزة (أسس Lyapunov) مع نقطة فريدة من النوع المركزي. في النظام غير الخطي حيث ينشأ تركيز غير مستقر، من الممكن ولادة دورة الحد. يمكن تتبع هذا التحول بسهولة في نظام "نموذجي":

(8.3)

يظهر حدوث دورة الحد في النظام (8.3) بشكل تخطيطي في المخطط البارامترى للطور في الشكل. 8.6.

أرز. 8.6. فوق الحرج (فوق الحرج) تشعب أندرونوف-هوبف. إثارة خفيفة. في مع> 0 تحدث تذبذبات ذاتية، يزداد اتساعها مع الزيادة مع.

حالة إعادة ل 1,2 = 0، وإيم ل 1,2 ¹ 0، يتوافق مع التشعب أندرونوف-هوبف أو تشعب ولادة (اختفاء) دورة الحد.تمت دراسة التشعب لأول مرة بواسطة أ.أ. أندرونوف لهذه القضية ن= 2 وقام E. Hopf بتعميمها على الأنظمة ذات الأبعاد العشوائية. (Andronov A.A.، Witt A.A.، Khaikin S.E. نظرية التذبذبات. M.، Nauka، 1981؛ Hopf E.، 1942)

هناك نوعان من تشعب أندرونوف-هوبف. لقد قمنا للتو بفحص التشعب فوق الحرج (الإثارة الناعمة للتذبذبات الذاتية). من الممكن أيضًا التشعب دون الحرج (الإثارة الشديدة للتذبذبات الذاتية). في هذه الحالة، مع قيمة التشعب للمعلمة، يفقد التركيز المستقر الاستقرار بسبب "التصاق" دورة الحد غير المستقرة فيه (الشكل 8.7). يصبح التركيز غير مستقر، ويمكن لدورة محدودة ذات سعة كبيرة أن تصبح جاذبة.

النظام "النموذجي" (انظر المحاضرة 6)، الذي يصف ولادة دورة الحد في ظل الإثارة الشديدة، هو النظام:

(8.4)

وبمساواة الطرف الأيمن من المعادلة الأولى بالصفر، نحصل على قيم ثابتة ص:

فرع ص= 0 مستقر عند ج < 0 и неустойчива при ج > 0.

في مع> -1 حل ثابت - دورة الحد المستقر.

في 1<مع<0 стационарное решение - دورة الحد غير المستقرة.

دعونا نفكر فيما يحدث إذا تحركت على طول المعلمة معبدءًا بالقيم السالبة (الشكل 8.8). في البداية هناك حالة ثابتة واحدة مستقرةص= 0، لا تتردد. فيج> -1 هناك أيضًا دورة حدية مستقرة، لكن النظام لا يترك حالته الثابتة المستقرة. ومع ذلك، بعد معتصبح إيجابية، وتصبح الحالة المستقرة غير مستقرة، وهناك قفزة حادة إلى دورة حدية مستقرة. تبدأ الاهتزازات ذات السعة الكبيرة على الفور في النظام. إذا انتقلنا من القيم الإيجابية معإلى السلبية، وتستمر التذبذبات ذات السعة الكبيرة حتى معلن تصبح أقل من -1، ثم تختفي فجأة. وهكذا عند -1< مع< 0 قد يكون هناك نوعان مختلفان من السلوك. أي واحد يتم تنفيذه يعتمد على خلفية النظام. وتسمى هذه الظاهرة تأثير التباطؤ.

عند زيادة المعلمة معوانتقاله إلى الصفر، تظهر فجأة تذبذبات ذاتية مستقرة ذات سعة وتردد محدودين. لقيم المعلمات المتوسطة معهناك نوعان من السلوك المستدام (جاذبان) - حالة ثابتة مستقرة ودورة حد مستقرة.

وينفري ( وينفريأ.ت.) مناطق محددة يمكن فيها وضعين: نقطة راحة ثابتة ودورة حدية، - الثقب الأسود(الشكل 8.8 ب) . في هذا النطاق من المعلمات، من الممكن تطبيق اضطراب على النظام التذبذبي بحيث يقع في منطقة جذب نقطة السكون، الأمر الذي سيؤدي إلى توقف التذبذبات. على وجه الخصوص، يظهر هذا في معادلات هودجكين-هكسلي، التي تمثل نموذجًا لتوصيل النبضات العصبية (انظر أدناه).

بروسيلاتور.أبسط مثال كلاسيكي على وجود التذبذبات الذاتية في نظام التفاعلات الكيميائية هو نموذج "Brussellator" ثلاثي الجزيئات، الذي اقترحه بريجوجين وليفيفر في بروكسل (1965). وكان الهدف الرئيسي في دراسة هذا النموذج هو إنشاء أنواع نوعية من السلوك المتوافقة مع القوانين الأساسية للحركية الكيميائية والبيولوجية.

وبهذا المعنى، يلعب المذبذب الأزرق دور النموذج الأساسي، مثل المذبذب التوافقي في الفيزياء، أو نموذج فولتيرا في الديناميكيات السكانية. في الجزء الثاني من المحاضرات سوف نركز على الخصائص الزمانية المكانية للنظام الموزع، والعنصر المحلي منه هو Brusselator. سننظر هنا في خصائص جهاز Brusselator كنظام ذاتي التأرجح.

يحتوي Brusselator على أبسط تطبيق لعدم الخطية المكعبة من خلال التفاعل الكيميائي

2X + ي ® 3X(8.5)

على الرغم من أن المرحلة الثلاثية الجزيئية في الحركية الكيميائية ليست شائعة مثل العمليات ثنائية الجزيئية، إلا أن التعبيرات الخاصة بمعدل عدد من التفاعلات الكيميائية الحيوية في حالات معينة يمكن اختزالها إلى الشكل المكعب. على سبيل المثال، نعطي التسلسل التالي من التفاعلات الأنزيمية:

X + ه ® السابق

السابق + ي ® س ص

إكسي+ X ® السابق 2 ي

ومن المفترض هنا أن الإنزيم هيحتوي على ثلاثة مراكز تحفيزية على الأقل قادرة على تثبيت جزيئين في وقت واحد Xوجزيء واحدي. إذا كانت المجمعات الناتجة تتحلل بمعدل مرتفع بما فيه الكفاية، وكانت الإنزيمات موجودة بكميات صغيرة، فمن السهل إظهار أنه يمكن تقليل تسلسل التفاعلات بالكامل إلى خطوة واحدة، مما يعطي مصطلحًا غير خطي مثل X 2 يفي التعبير عن معدل التفاعل.

يمثل Brusselator المخطط التالي للتفاعلات الكيميائية الافتراضية:

هنا أ, في- المواد الأولية، ج, ر- منتجات، X, ي- مواد وسيطة.

دع المنتجات النهائية معو رتتم إزالتها على الفور من مساحة التفاعل. وهذا يعني أن الثوابت معكوسة ك - 3 = ك - 4 = 0. إذا كانت الركيزة أهو في الزائدة ك - 1 = 0. ولنفترض ذلك أيضًا ك - 2 = 0. قيم الثوابت المتبقية تساوي واحدًا. ثم يتم وصف مخطط التفاعل 9.2 (في حالة نظام النقاط) بواسطة نظام المعادلات:

النموذج (8.5) له نقطة واحدة خاصة بإحداثياتها:

. (8.7)

دعونا نتفحص الحل الثابت (8.6) لتحقيق الاستقرار باستخدام طريقة ليابونوف. دعونا نقدم متغيرات تميز الانحرافات عن النقطة المفردة:

النظام الخطي له الشكل:

معادلة مميزة

ل 2 + (أ 2 + 1 - ب) ل + أ 2 = 0

له جذور:

تذكر أن النقطة المفردة تكون مستقرة إذا كانت الأجزاء الحقيقية لجذور المعادلة المميزة سالبة. من التعبير (8.7) يتضح أنه متى ب< 1+ أ 2 نقطة المفرد (8.6) مستقرة. لو ب> 1 + أفي الشكل 2، تصبح النقطة المفردة غير مستقرة، والنظام (8.5) لديه دورة حدية مستقرة. معنى ب=1+ أ 2 هو التشعب. إذا كانت القيمة بيتجاوز عتبة التشعب قليلاً فقط، وتكون التذبذبات الذاتية في النظام شبه متناغمة بطبيعتها. وهكذا يكون Brusselator عندما يتم استيفاء الشرط

ب> 1 + أ 2 (8.8)

هو نظام التأرجح الذاتي. تظهر صورة الطور لـ Brusselator لقيم المعلمات المختلفة في الشكل. 8.9

نقدم هنا لمحة موجزة عن العديد من النماذج "الناجحة" للعمليات البيولوجية التذبذبية. سيتم مناقشة بعض العمليات التذبذبية بمزيد من التفصيل في المحاضرات 9، 11، 12.

نموذج للعمليات المظلمة لعملية التمثيل الضوئي.

كان أحد النماذج الأولى التي تصف العملية التذبذبية في النظام الحي هو نموذج العمليات المظلمة لعملية التمثيل الضوئي، الذي اقترحه ودرسه د.س. تشيرنافسكي وزملاؤه (1967). يعتبر النموذج مثالا لنظام من الدرجة الثانية ذو جوانب تربيعية على الجانب الأيمن، تنشأ فيه تذبذبات ذاتية (توجد دورة حدية) ويتيح دراسة تحليلية كاملة (بيليوستينا، 1967).

من المعروف أنه في ظل ظروف النهار والليل، تتغير شدة عملية التمثيل الضوئي، أي معدل إطلاق الأكسجين وامتصاص ثاني أكسيد الكربون، بشكل دوري (الشكل 8.10). أ). إذا تم وضع النبات في ظروف الإضاءة المستمرة، فإن دورية شدة التمثيل الضوئي مع فترة عدة ساعات تستمر لفترة طويلة. على ما يبدو، فإن المصنع لديه إيقاع داخلي خاص به، متزامنا مع التأثيرات الخارجية الدورية.

تذكر أن عملية التمثيل الضوئي تتضمن دورات خفيفة ومظلمة من التفاعلات الكيميائية. الأول ينطوي على امتصاص طاقة الكمات الضوئية، ومن خلال سلسلة من المراحل المتوسطة، يؤدي إلى تكوين مركبات كيميائية منخفضة الطاقة عالية وجزيئات ATP الغنية بالطاقة. وتستخدم هذه المواد في الدورة المظلمة (دورة كالفين)، والتي لا يتدخل فيها الضوء بشكل مباشر. هنا، يتم تقليل ثاني أكسيد الكربون CO 2 بمساعدة المواد الغنية بالطاقة والجهات المانحة للهيدروجين التي تم الحصول عليها في الدورة الضوئية، ويتم تحويلها إلى الكربوهيدرات - الفركتوز والجلوكوز (الشكل 8.11).

تتضمن الدورة كربوهيدرات ذات محتويات كربون مختلفة (يشير المؤشر أدناه إلى عدد ذرات الكربوهيدرات في الجزيء). جميع السكريات ثلاثية الكربون لها الاسم الشائع ثلاثي ( مع 3)، خمسة الكربون ( مع 5) - البنتوزات، ستة الكربون ( مع 6) - السداسيات. الدورة مغلقة، أي. المادة التي يضاف إليها ثاني أكسيد الكربون في البداية (مستقبل ثاني أكسيد الكربون، المشار إليه في الشكل 8.8 بالرمز مع 5) يتم تجديده نتيجة للتفاعل. أبسط السكريات - الثلاثيات - ترتبط مباشرة بالدورة الضوئية؛ أما السكريات الأخرى فلا ترتبط بالدورة الضوئية. جميع التفاعلات في الدورة، باستثناء التثبيت الأولي لثاني أكسيد الكربون على الريبولوز، هي تفاعلات ثنائية الجزيئية، ويتم وصف اعتماد معدل التفاعل على التركيز بمصطلحات من الدرجة الثانية.

ولتبسيط النظام، تم تحديد مجموعات من المواد، والتي تحدث التفاعلات بينها بسرعة وبشكل عكسي، وهي السكريات الخفيفة (كربوهيدرات ثلاثية الكربون) والسكريات الثقيلة سداسية الكربون. تم تحديد التركيز الكلي للأول بشكل تقليدي من 3، وثانيا مع 6 .

وكان من المفترض أن الربح من السكريات الثقيلة مع 6ـ يمكن إجراؤها عن طريق ربط الرئتين مع 3. ويحدث فقدانها، وكذلك فقدان السكريات الثقيلة، نتيجة للتفاعل الجزيئي للسكريات الثقيلة والخفيفة. هناك أيضًا تدفق للمنتج مع 3 في مجال التفاعل بسبب عمليات مشابهة كيميائيا (تحلل السكر، والتنفس). تؤدي هذه الافتراضات إلى نظام المعادلات:

(8.9)

تمثل المتغيرات تركيزات الرئة الطبيعية ( س) وثقيل ( ذ) السكريات. في الربع الموجب توجد حالة توازن واحدة ذات إحداثيات (1،1). يتم تحديد الخطوط المتساوية للظلال الأفقية من المعادلة

وخطوط تساوي الزوايا العمودية مأخوذة من المعادلة

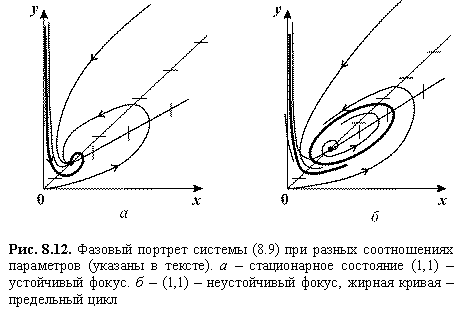
في التين. يوضح الشكل 8.12 صور الطور للنظام. هذا تركيز مستقر (الشكل 8.12 أ). في- تركيز غير مستقر محاط بدورة محدودة (الشكل 8.12 ب).

تقلبات في تحلل السكر.

المثال الكلاسيكي للتفاعل الكيميائي الحيوي المتذبذب هو تحلل السكر. في عملية تحلل السكر، يتم تكسير الجلوكوز والسكريات الأخرى، بينما يتم تحويل المركبات التي تحتوي على ستة جزيئات كربون إلى أحماض ثلاثية الكربوكسيل، تحتوي على ثلاثة جزيئات كربون. بسبب الطاقة الحرة الزائدة في عملية تحلل السكر، يتم تشكيل جزيئين من ATP لكل جزيء من السكر سداسي الكربون. الدور الرئيسي في توليد التقلبات الملحوظة في تراكيز مكونات التفاعل: الفركتوز 6 فوسفات، الفركتوز 1،6 فوسفات و NAD المختزل ( نيكوتيمينامين أدنين ثنائي النوكليوتيد) يلعب إنزيمًا رئيسيًا في مسار تحلل السكر- فسفوفركتوكيناز (PFK).يظهر مخطط التفاعل المبسط في الشكل. 8.13:

في الرسم البياني [GL] - الجلوكوز، F6P - الفركتوز 6 فوسفات- ركيزة التفاعل الرئيسي، FDF هو نتاج هذا التفاعل، وهو الركيزة في المرحلة التالية. يتم تحفيز كلا التفاعلين بواسطة الإنزيمات. في المتغيرات عديمة الأبعاد، يمكن كتابة نظام المعادلات التي تصف التفاعلات على النحو التالي:

وهنا يتم كتابة اعتمادات معدلات التفاعل على المتغيرات بصيغة ميكايليس-مينتن (مونوت) كما ورد في المعادلة (8.10) في حالة استيفاء الشروط:كمكس>> س, ك بلدي>> ذ, يمكنك تغيير المتغيرات 8.14

أرز.8.14. X) وثنائي فوسفات الفركتوز ( في أ- عملية غير تذبذبية (عقدة على مستوى الطور)، α= 0.25; ص = 1. ب– التذبذبات المبللة (التركيز المستقر على مستوى الطور) α = 4؛ص = 0.2

أرز.8.14. نموذج تحلل السكر (8.10). حركية التغيرات في تركيزات الفركتوز 6 فوسفات ( X) وثنائي فوسفات الفركتوز ( في) (يمين) وصورة طور النظام (يسار) لقيم مختلفة لمعلمات النظام، الخامس- تذبذبات ذات سعة وطور ثابتين، قريبة من التوافقية (دورة الحد على مستوى الطور)، α = 6؛ص = 0.2. ز- تذبذبات الاسترخاء ذات السعة والطور الثابتين (دورة محدودة ذات شكل مثلث تقريبًا على مستوى الطور) α = 8؛ص = 0.5

ومن المثير للاهتمام أن التفاعلات التذبذبية في نظام تحلل السكر تم التنبؤ بها لأول مرة باستخدام نموذج رياضي (هيغينز، 1964)، وبعد ذلك فقط تم تسجيلها تجريبيًا باستخدام طريقة قياس الطيف الضوئي التفاضلي في مختبر B. Chance (1966).

تقلبات الكالسيوم داخل الخلايا.

في العديد من أنواع الخلايا الحية، لوحظت تقلبات في تركيز الكالسيوم داخل الخلايا، والتي يمكن أن تختلف مدتها من 0.5 إلى 10 دقائق. يظهر في الشكل أبسط رسم تخطيطي للعمليات التي تؤدي إلى تقلبات الكالسيوم المحددة هرمونيًا، والتي أساسها هو إطلاق الكالسيوم الناجم عن الكالسيوم من الخلية. 8.15. تمت ملاحظة مثل هذه التذبذبات لأول مرة من قبل إندو وآخرين (1970) على خلايا العضلات الهيكلية، وفابياتو (1975) على خلايا الشبكة الإندوبلازمية العضلية لقلب البقر، وبعد ذلك من قبل العديد من الباحثين الآخرين.

مخطط ونموذج العمليات، المقترح والمرجع السابق.إيسانا في . يعتبر تدفق وتدفق الكالسيوم إلى الخلية عبر غشاء البلازما (ثوابت المعدل الخامس 1 و الخامس 2، على التوالي)؛ إطلاق الكالسيوم المنشط هرمونيًا من حوض السباحة (معدل الخامس 3)؛ النقل النشط للكالسيوم عصاري خلوي في حوض السباحة، ( الخامس 4) إطلاق الكالسيوم من حوض السباحة، والذي يتم تنشيطه بواسطة الكالسيوم العصاري الخلوي ( الخامس 5)؛ التدفق الحر للكالسيوم من البركة إلى العصارة الخلوية ( الخامس 6). يتكون النموذج من معادلتين تفاضليتين

(8.11)

دورات الخلية.

خلال دورة الحياة، تتضاعف الخلية محتوياتها وتنقسم إلى قسمين. في جسم الثدييات، يتم إنتاج ملايين الخلايا الجديدة كل ثانية للحفاظ على الحياة. يتجلى خلل تنظيم تكاثر الخلايا في شكل سرطان. وقد أثار هذا اهتمامًا كبيرًا بدراسة ونمذجة آليات تنظيم انقسام الخلايا.

يظهر مخطط دورة الخلية في الشكل. 8.17. تتكون دورة الخلية من فترتين: الانقسام ( م-المرحلة) تتضمن فصل المادة النووية المضاعفة سابقًا، وتقسيم النواة وتقسيم الخلية نفسها - التحريك الخلوي ويستغرق حوالي ساعة. فترة أطول بكثير بين الانقسامين تشغلها الطور البيني، والذي يتضمن مرحلة النمو ز 1، مرحلة تكرار الحمض النووي ( س)، مرحلة الإعداد للقسمة ز 2. يتم تنظيم دورة الخلية (الشكل 8.17) بواسطة الجينات وبروتينات الإنزيمات من فئتين رئيسيتين.

تحفز كينازات البروتين المعتمدة على السيكلين (Cdks) سلسلة من الأحداث عن طريق فسفرة البروتينات الفردية. ترتبط السيكلينات، التي يتم تصنيعها وتحللها مع كل دورة تقسيم جديدة، بجزيئات Cdk وتتحكم في قدرتها على الفسفرة. بدون السيكلين Cdk، فهي غير نشطة. يختلف عدد هذه الجزيئات التنظيمية باختلاف أنواع الخلايا.

في انقسام خلايا الخميرة، يتم لعب الأدوار الرئيسية بواسطة Cdk واحد وتسعة سيكلينات، والتي تشكل تسعة مجمعات cyclin-Cdk مختلفة. في الثدييات الأكثر تعقيدًا، تمت دراسة ستة أقراص مضغوطة وواحد ونصف دستة من السيكلينات. التحكم في خروج الخلية ز 1، و زيتم تنفيذ مرحلتين بواسطة عامل المروج س-المرحلة (SPF) وعامل المروج م- الأطوار (MPF) وهي عبارة عن ثنائيات متغايرة. هناك نقطة تفتيش خاصة لدورة الخلية (البداية) ومنها ينتهي النمو ( زالمرحلة 1) وتبدأ عملية تخليق الحمض النووي.

تم اقتراح نموذج عملية بسيط بواسطة تايسون (1995). يُفترض وجود عامل النسخ SBF، والذي قد يكون نشطًا سأ والسلبي سط تشكيل. يتم تحويله إلى شكله النشط بواسطة عمل cyclin Cln ( ن) وبدء كيناز (Cdc28-Cln3) ( أ) ويتم تعطيله بواسطة مادة أخرى ( ه). يتم إنتاج Cyclin عن طريق تنشيط SBF ويتحلل. يتم تنشيط SBF بواسطة Chu وStart kinase ويتم تعطيله بواسطة الفوسفاتيز. نموذج العملية بدون أبعاد له الشكل:

(8.13)

يحتوي النموذج على واحد أو ثلاثة حلول ثابتة (اثنان مستقران) اعتمادًا على قيم المعلمات ومع زيادة المعلمةأ(أثناء نمو الخلية) يصف تحول النظام من ز 1 في سمرحلة.

إن إضافة معادلتين لهما صيغة مماثلة يسمح لنا أيضًا بوصف التبديل من ز 2 في مرحلة الانقسام م. يحتوي النموذج الكامل، الذي يأخذ في الاعتبار الإنزيمات التنظيمية الأخرى في الأشكال المفسفرة والمنزوعة الفسفور، على 9 معادلات غير خطية (Novak, Tyson 1993) ويصف جيدًا حركية انقسام البويضات. النمو. مع الاختيار المناسب للمعلمات، فإنه ينطبق على وصف تقسيم أنواع أخرى من الخلايا.

تم تخصيص عدد كبير من الأعمال لمحاولات محاكاة التأثيرات الدورية على دورة الخلية من أجل تحسين معايير العلاج الإشعاعي بالأشعة السينية أو العلاج الكيميائي عند التأثير على الخلايا السرطانية.

في الأدبيات الحديثة عن علم الأحياء الرياضي، يتم النظر في مئات الأنظمة ذاتية التأرجح على مستويات مختلفة من تنظيم الطبيعة الحية. مما لا شك فيه أن الطبيعة المتذبذبة للعمليات هي اختراع تطوري للطبيعة، ودورها الوظيفي له عدة جوانب مختلفة.

أولاً، تتيح التذبذبات فصل العمليات في الوقت المناسب، عندما تحدث عدة تفاعلات مختلفة في حجرة خلية واحدة في وقت واحد، مما ينظم فترات النشاط المرتفع والمنخفض للأيضات الفردية. ثانيًا، تحمل خصائص التذبذبات، ومداها ومرحلتها، معلومات معينة ويمكن أن تلعب دورًا تنظيميًا في سلسلة من العمليات التي تحدث على مستوى الخلية والكائن الحي. أخيرًا، تعمل الأنظمة التذبذبية (المحتملة أو الفعلية) كعناصر محلية للوسائط النشطة الموزعة القادرة على التنظيم الذاتي الزماني المكاني، بما في ذلك عمليات التشكل. وسنتناول هذا الدور للأنظمة التذبذبية بالتفصيل في الجزء الثاني من المحاضرات.

الأدب

أندرونوف أ.أ.، ويت أ.أ.، كايكين إس.إي. نظرية التذبذب. م.، ناوكا، 1981.

بيليوستينا إل.إن.، كوكينا جي.إيه. دراسة نوعية لمعادلات التمثيل الضوئي. - فى السبت. العمليات التذبذبية في النظم البيولوجية والكيميائية. م.، ناوكا، 1967

Glensdorf P.، Prigozhin I. النظرية الديناميكية الحرارية للهيكل والاستقرار والتقلبات. م، 1978

Nikolis J، Prigozhin I. التنظيم الذاتي في أنظمة عدم التوازن. م، مير، 1979

Chernavsky D.S.، Chernavskaya N.M. على التقلبات في ردود الفعل المظلمة لعملية التمثيل الضوئي. - فى السبت. العمليات التذبذبية في النظم البيولوجية والكيميائية. م، العلوم، 1967

Dupont G. وGoldbetter A. رؤى نظرية حول أصل تذبذبات الكالسيوم الناتجة عن الإشارة، في Goldbetter A. (ed). الإشارات من خلية إلى خلية: من التجارب إلى النماذج النظرية. أكاد. الصحافة، لندن، ص. 461-474، 1989

Dupont G. and Goldbetter A. التذبذبات وموجات الكالسيوم السيتوسوليك: رؤى من النماذج النظرية. المقالات الحيوية، 14، 485-493، 1992

هيغينز ج. آلية كيميائية للتذبذبات في الوسطيات المحللة للسكر في خلايا الخميرة. بروك. نات. أكاد. الخيال العلمي. الولايات المتحدة الأمريكية، الإصدار 51، 1954

هيغينز ج. نظرية ردود الفعل المتذبذبة. عمل. الكيمياء. V.59، N5، 1967

Hopf E. Abzweilung einerperiodischen Losung von einer stationaren Losung eines Differentialsystems (تشعب الحل الدوري من الحل الثابت لنظام المعادلات التفاضلية) Ber. الرياضيات والفيزياء. كوالالمبور. ساكس. أكاد. ويس. لايبزيغ 94، 3-22، 1942

نوفاك بي، تايسون ج.ج. نمذجة دورة انقسام الخلايا: تحفيز الطور M، التذبذب والتحكم في الحجم، J. Theor. بيول. 165، 101-104، 1993

سوموجي آر، ستوكين ج.و. يمكن تفسير تذبذبات الكالسيوم الناجمة عن الهرمونات في خلايا الكبد من خلال نموذج واحد بسيط. جي بيول. كيم.266، 11068-11077، 1991

Prigozhine I.R.، Lefebre R. التماثل، وكسر عدم الاستقرار، والأنظمة غير المبددة. تشي. فيز، 48، 1665-1700، 1968

وينفري ايه تي. هندسة الزمن البيولوجي. سبرينغر، 1980

دع بعض الأنظمة الديناميكية تعطى من خلال حل المعادلات لهذا النظام في ر → ∞لا تعطى دائما من خلال حالة التوازن. لذلك، على سبيل المثال، بشرط الحصول على الجذور التخيلية للمعادلة المميزة المقابلة، يتم وصف سلوك النظام على أنه تذبذبات غير مخمدة ذات سعة ثابتة، أي أن الحل هو الدوال س(ر+ت)=س(ر), ص(ر+T)=ص(ر). في هذه الحالة يقولون أنه في النظام هناك دورة الحد المستقر. يظهر الشكل 1 صورة نموذجية لسلوك المحاليل بالقرب من دورة الحد. 1
الشكل 1 - دورة الحد المستقرة يتم "جرح" مسارات المرحلة من الداخل والخارج حول الدورة. بغض النظر عن البيانات الأولية، ستحدث تذبذبات ذات سعة وتردد ثابتين في النظام - ما يسمى التذبذبات الذاتية. أنواع الدورات الحدية:

مستقرة - مسارات قريبة "الرياح" على الدورة عند ر → ∞(الصورة 2)؛
شبه مستقرة - مسارات تقع على جانب واحد من الدورة - "تهب" عليها متى ر → ∞وأولئك الذين على الجانب الآخر "يخرجون" من الدورة (الشكل 3) ؛
غير مستقر - المسارات القريبة "تنحرف" عن الدورة متى ر → ∞(الشكل 4).

أرز. 2- دورات مستقرة. أرز. 3 - شبه مقاومة. أرز. 4 - غير مستقر لسوء الحظ، لا توجد طرق فعالة معممة لتحديد استقرار الدورات الحدية. واحد منهم يعتمد على استخدام وظيفة التقليد.

وظيفة التقليد

فكرة بناء وظيفة التقليد هي كما يلي. يتم رسم شعاع يتقاطع بوضوح مع الدورة النهائية والمسارات القريبة. على سبيل المثال، لنرسم شعاعًا الزراعة العضويةتنبثق من نقطة واحدة عنوالتي تقع داخل دورة الحد (الشكل 5). دعونا ندخل الإحداثيات صعلى طول هذا الشعاع. النظر في مسار مغادرة هذه النقطة أ، تابعة للشعاع. دع هذا المسار أولًا يتقاطع مع الشعاع عند هذه النقطة في. دعونا نقدم الوظيفة ص ب = و(ص أ)، والتي لكل نقطة مع الإحداثيات ص أيطابق إحداثيات نقطة في. يترك ص ن- التنسيق نتقاطع المسار مع الشعاع. ثم ص ن+1 = و(ص ن)، وتتوافق دورة الحد مع النقطة الثابتة لهذا التعيين ص* = و(ص*). لو ص ن → ص*للجميع ص طتابعة للحي ص*، فإن دورة الحد ستكون مستقرة.

الشكل 5 - بناء دالة التقليد تبين أن فكرة بناء دالة التقليد كانت مثمرة للغاية لدراسة الأنظمة غير الخطية، وخاصة ذات الرتبة الأعلى (بعد مساحة الطور ن>2). يسمى تعميم النهج الموصوف طريقة قسم بوانكاريه. وفي الوقت نفسه، الانتقال إلى أنظمة ذات عدد كبير من الأبعاد، بدلاً من الشعاع الزراعة العضويةينبغي النظر في بعض الطائرة المفرطة. على سبيل المثال، في الحالة ثلاثية الأبعاد نأخذ في الاعتبار النقاط P0، P1، P2، ...، Pnكأقسام من مسار مع الطائرة س(الشكل 6). تسمى التحولات التي تأخذ نقطة إلى النقطة التالية خريطة بوانكاريه: ف ن + 1 = تي(ف ن)

الشكل 6 - التمثيل التخطيطي لقسم بوانكاريه تعمل طريقة قسم بوانكاريه على تبسيط دراسة الأنظمة الديناميكية المستمرة لثلاثة أسباب على الأقل:

يتم تقليل عدد متغيرات الطور بمقدار واحد؛
يتم استبدال المعادلات التفاضلية بمعادلات الفرق من النموذج س ط (ك + 1) = و (س ط (ك)))، ط = 1،2، ...، ن،والتي هي أسهل بكثير للبحث؛
يتم تقليل كمية البيانات التي سيتم معالجتها بشكل حاد، حيث يمكن إهمال جميع النقاط الموجودة على المسار تقريبًا.

بالإضافة إلى ذلك، العديد من أنظمة المعادلات التفاضلية تولد تعيينات مماثلة. لذلك، غالبًا ما تُعتبر التعيينات أحادية البعد وثنائية الأبعاد بمثابة نماذج مبسطة لعمليات مختلفة. تحقق أيضا: